Содержание
Урок 1
Архитектура IBM PC
Минимальной единицей информации в компьютере является бит. Бит может быть выключен, так что его значение есть нуль, или включен, тогда его значение равно единице. Единственный бит не может представить много информации в отличие от группы битов. Группа из восьми битов представляет собой байт. Восемь битов обеспечивают основу для двоичной арифметики и для представления символов, таких как буква A или символ *. Восемь битов дают 256 различных комбинаций включенных и выключенных состояний: от «все выключены» (00000000) до «все включены» (11111111). Например, сочетание включенных и выключенных битов для представления буквы A выглядит как 01000001, а для cимвола * - 00101010 (это можно не запоминать). Каждый байт в памяти компьютера имеет уникальный адрес, начиная с нуля. Может появится вопрос: «откуда компьютер «знает», что значения бит 01000001 представляют букву A?» Когда на клавиатуре нажата клавиша A, система принимает сигнал от этой конкретной клавиши в байт памяти. Этот сигнал устанавливает биты в значения 01000001. Можно переслать этот байт в памяти и, если передать его на экран или принтер, то будет сгенерирована буква A. По соглашению биты в байте пронумерованы от 0 до 7 справа налево, как это показано для буквы A:
Номера бит: 7 6 5 4 3 2 1 0
Значения бит: 0 1 0 0 0 0 0 1
16-битовое (двухбайтовое) поле называется словом. Биты в слове пронумерованы от 0 до 15 справа налево, как это показано для букв PC:
Номера бит: 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 Значения бит: 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1
ASCII КОД
Для целей стандартизации в микрокомпьютерах используется aмериканский национальный стандартный код для обмена информацией ASCII (American National Standard Code for Information Interchange). Именно по этой причине комбинация бит 01000001 обозначает букву A. Наличие стандартного кода облегчает обмен данными между различными устройствами компьютера. 8-битовый рассширенный ASCII-код, используемый в PC обеспечивает представление 256 символов, включая символы для национальных алфавитов.
Двоичные числа
Так как компьютер может различить только нулевое и единич ное состояние бита, то он работает системе исчисления с базой 2 или в двоичной системе. Фактически бит унаследовал cвое название от английского «BInary digiT» (двоичная цифра). Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число содержащее все единичные биты:
Позиционные веса: 128 64 32 16 8 4 2 1 Включенные биты: 1 1 1 1 1 1 1 1
Самый правый бит имеет весовое значение 1, следующая цифра влево - 2, следующая - 4 и т.д. Общая сумма для восьми еди ничных битов в данном случае составит 1 + 2 + 4 + … + 128, или 255 (2 в восьмой степени - 1). Для двоичного числа 01000001 единичные биты представляют значения 1 и 64, т.е. 65. Но 01000001 представляет также букву A! Действительно, здесь момент, который необходимо четко уяснить. Биты 01000001 могут представлять как число 65, так и букву A: - если программа определяет элемент данных для арифметических целей, то 01000001 представляет двоичное число, эквивалентное десятичному числу 65; - если программа определяет элемент данных (один или более смежных байт), имея в виду описательный характер, как, например, заголовок, тогда 01000001 представляет собой букву. При програмировании это различие становится понятным, так как назначение каждого элемента данных определено. Двоичное число неограничено только восьмью битами. Так как процессор 8086 использует 16-битовую архитектуру, oн автоматически оперирует с 16-битовыми числами. (2 в степени 16) минус 1 дает значение 65535, а немного творческого программирования позволит обрабатывать числа до 32 бит ((2 в степени 32) минус 1 равно 4294967295) и даже больше.
Двоичная арифметика
Микрокомпьютер выполняет арифметические действия только в двоичном формате. Поэтому программист на языке ассемблера должен быть знаком с двоичным форматом и двоичным сложением: 0 + 0 = 0 1 + 0 = 1 1 + 1 = 10 1 + 1 + 1 = 11 Обратное внимание на перенос единичного бита в последних двух операциях. Теперь, давайте сложим 01000001 и 00101010. Букву A и символ *? Нет, число 65 и число 42:
Двоичные Десятичные
01000001 65
00101010 42
01101011 107
Проверьте, что двоичная сумма 01101011 действительно равна 107. Рассмотрим другой пример:
Двоичные Десятичные
00111100 60
00110101 53
01110001 113
Отрицательные числа
Все представленные выше двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого (старшего)разряда. Отрицательные двоичные числа содержат единичный бит в старшем разряде и выражаются двоичным дополнением. Т.е., для представления отрицательного двоичного числа необходимо инвертировать (0 заменить на 1, а 1 замнить на 0) все биты и прибавить 1. Рассмотрим пример:
Число 65: 01000001
Инверсия: 10111110
Плюс 1: 10111111 (равно -65)
Если прибавить единичные значения к числу 10111111, 65 не получится. Фактически двоичное число считается отрицательным, если его старший бит равен 1. Для определения абсолютного значения отрицательного двоичного числа, необходимо повторить предыдущие операции: инвертировать все биты и прибавить 1:
Двоичное значение: 10111111
Инверсия: 01000000
Плюс 1: 01000001 (равно +65)
Сумма +65 и -65 должна составить ноль:
01000001 (+65)
10111111 (-65)
(1)00000000
Все восемь бит имеют нулевое значение. Перенос единичного бита влево потерян. Однако, если был перенос в знаковый pазряд и из разрядной сетки, то результат является кор ректным. Двоичное вычитание выполняется просто: инвентируется знак вычитаемого и складываются два числа. Вычтем, например, 42 из 65. Двоичное представление для 42 есть 00101010, и eго двоичное дополнение: - 11010110:
65 01000001
+(-42) 11010110
23 (i)00010111
Результат 23 является корректным. В рассмотренном примере произошел перенос в знаковый разряд и из разрядной сетки. Если справедливость двоичного дополнения не сразу понят на, рассмотрим следующие задачи: Какое значение необходимо прибавить к двоичному числу 00000001, чтобы получить число 00000000? В терминах десятичного исчисления ответом будет -1. Для двоичного рассмотрим 11111111:
00000001
11111111
Результат: (1)00000000
Игнорируя перенос (1), можно видеть, что двоичное число 11111111 эквивалентно десятичному -1 и соответственно:
0 00000000
-(+1) -00000001
-1 11111111
Можно видеть также каким образом двоичными числами пред cтавлены уменьшающиеся числа:
+3 00000011
+2 00000010
+i 00000001
0 00000000
-1 11111111
-2 11111110
-3 11111101
Фактически нулевые биты в отрицательном двоичном числе определяют его величину: рассмотрите позиционные значения нулевых битов как если это были единичные биты, сложите эти значения и прибавте единицу.
Шестнадцатиричное представление
Во многих случаях двоичное представление числа оказывается неудобным, так как запись числа осуществляется большим количеством цифр. Для сокращения записи числа в программирование довольно часто используют шестнадцатиричную систему счисления. Тогда каждая четвёрка бит, начиная с нулевого, может быть представленна в виде одной шестнадцатиричной цифры (от 0 до F).
Таблица перевода четвёрки битов в 16-ричную цифру:
bits hex dec 0000 0 0 0001 1 1 0010 2 2 0011 3 3 0100 4 4 0101 5 5 0110 6 6 0111 7 7 1000 8 8 1001 9 9 1010 A 10 1011 B 11 1100 C 12 1101 D 13 1110 E 14 1111 F 15
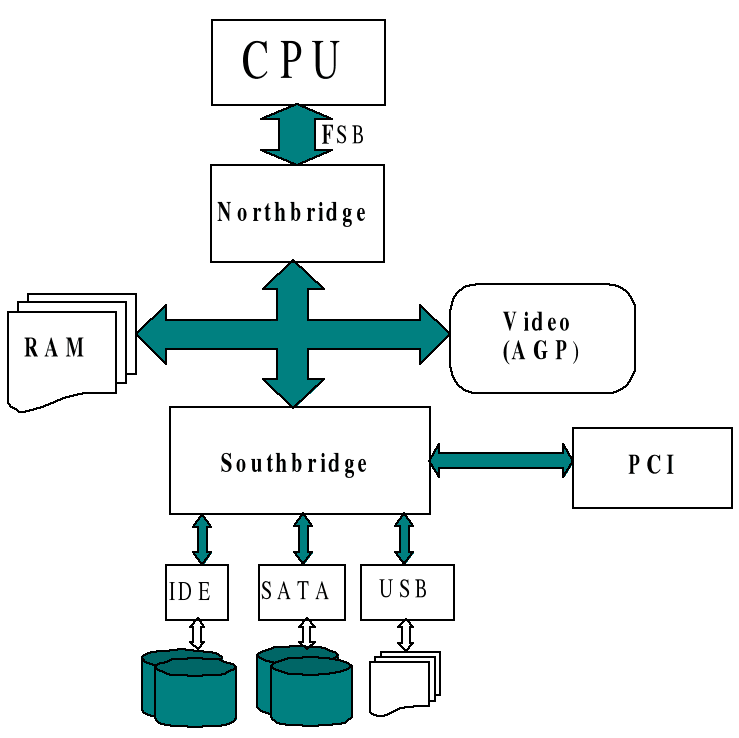
Устройство IBM PC
Процессор Intel 8086
Регистры
Всего в процессоре i8086 было 14 16-разрядных регистров: 4 регистра общего назначения (AX, BX, CX, DX), 2 индексных регистра (SI, DI), 2 указательных (BP, SP), 4 сегментных регистра (CS, SS, DS, ES), программный счётчик или указатель команды (IP) и регистр флагов (FLAGS, включает в себя 9 флагов). При этом регистры данных (AX, BX, CX, DX) допускали адресацию не только целых регистров, но и их младшей половины (регистры AL, BL, CL, DL) и старшей половины (регистры AH, BH, CH, DH), что позволяло использовать не только новое 16-разрядное ПО, но сохраняло совместимость и со старыми программами (правда, их необходимо было, по крайней мере, перекомпилировать). (с) http://ru.wikipedia.org/wiki/Intel_8086
Адресация памяти
 1-й вариант. Для того чтобы адресовать больший, чем i8080, объём памяти, потребовалось изменить способ адресации памяти. Ведь если использовать старые методы, когда адрес к ячейке памяти содержался в указательных регистрах, то пришлось бы увеличивать размер этих самых регистров, чтобы иметь возможность обращаться к большему объёму памяти. Поэтому для адресации 1 Мбайт памяти применили следующую схему. На шину адреса подавался физический адрес размером 20 бит, который формировался путём сложения содержимого одного из сегментных регистров (16 бит), умноженного на 16, с содержимым указательного регистра: таким образом, адресация ячейки памяти производилась по номеру сегмента и эффективному адресу ячейки в сегменте (называемому также смещением). Если результат сложения оказывался больше, чем 220 -1, то 21-й бит отбрасывался; такая процедура называется «заворачиванием» адреса (англ. address wraparound). Этот метод впоследствии (после появления защищённого режима) назвали реальным режимом адресации процессора, такой режим позволяет адресовать до 1 Мбайт памяти.
1-й вариант. Для того чтобы адресовать больший, чем i8080, объём памяти, потребовалось изменить способ адресации памяти. Ведь если использовать старые методы, когда адрес к ячейке памяти содержался в указательных регистрах, то пришлось бы увеличивать размер этих самых регистров, чтобы иметь возможность обращаться к большему объёму памяти. Поэтому для адресации 1 Мбайт памяти применили следующую схему. На шину адреса подавался физический адрес размером 20 бит, который формировался путём сложения содержимого одного из сегментных регистров (16 бит), умноженного на 16, с содержимым указательного регистра: таким образом, адресация ячейки памяти производилась по номеру сегмента и эффективному адресу ячейки в сегменте (называемому также смещением). Если результат сложения оказывался больше, чем 220 -1, то 21-й бит отбрасывался; такая процедура называется «заворачиванием» адреса (англ. address wraparound). Этот метод впоследствии (после появления защищённого режима) назвали реальным режимом адресации процессора, такой режим позволяет адресовать до 1 Мбайт памяти.
2-й вариант. Для того чтобы адресовать 1 мегабайт памяти (20 бит адреса) с использованием 16-битных регистров используется сегментирование. Старшие 4 бит адреса выводятся на отдельные контакты корпуса, а младшие 16 выводятся на совмещённую шину адреса-данных. Но граница сегмента не жёсткая, а плавающая. Для того чтобы адресовать нужный сегмент используются 16-битные регистры сегмента, значение которых сдвигается на 4 бита вверх и складывается с указательным 16-битным регистром. Полученное значение - 20 битный адрес памяти или устройства выводится на контакты. Если результат сложения оказывался больше чем 1 мегабайт, выводятся только младшие 20 бит адреса, 21-бит отбрасывается. Схема, показывающая работу реального режима адресации процессора Intel 8086 и выше
Таким образом, память разделяется на сегменты, размером 64 Кбайт каждый и начинающиеся с адреса, кратного 16 (граница параграфа); память в 1 Мбайт разделялась, таким образом, на 16 сегментов. Эти 16 сегментов называют страницами памяти. В компьютере, подобном IBM PC, последние 6 страниц (A, B, C, D, E, F) памяти (т. н. верхняя память — англ. upper memory) использовались для видеопамяти и BIOS-а, это ограничивало память, доступную пользователю, объёмом в 640 Кбайт (т. н. обычная память — англ. conventional memory; страницы 0~9).
На то время такой режим адресации обеспечивал множество преимуществ: ёмкость памяти могла составлять до 1 Мбайт, хотя команды оперировали 16-битными адресами; упрощалось использование отдельных областей памяти для программы, её данных и стека; упрощалась разработка устройств, совместимых друг с другом. (с) http://ru.wikipedia.org/wiki/Intel_8086
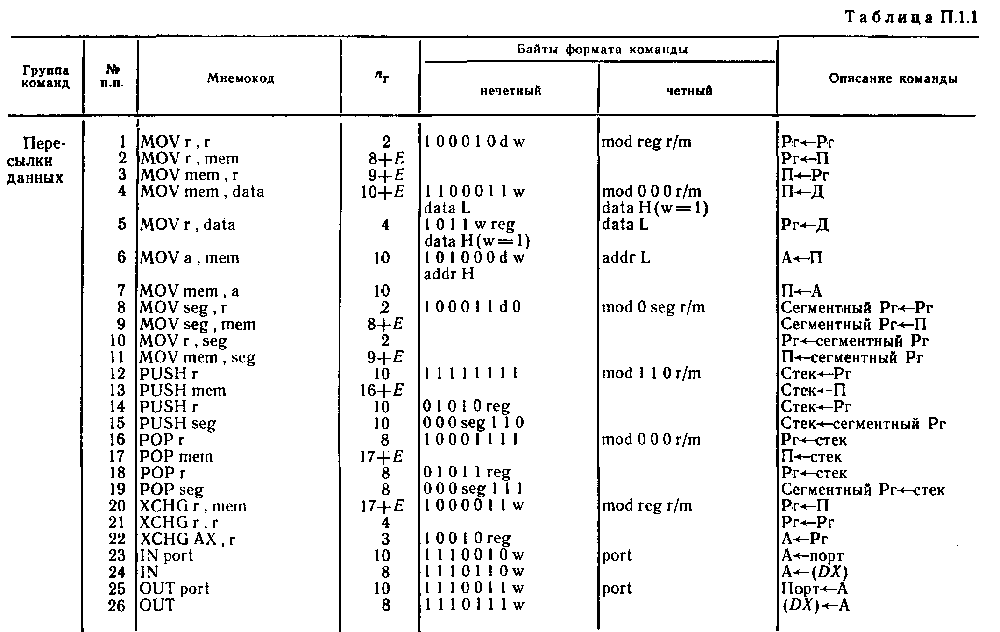
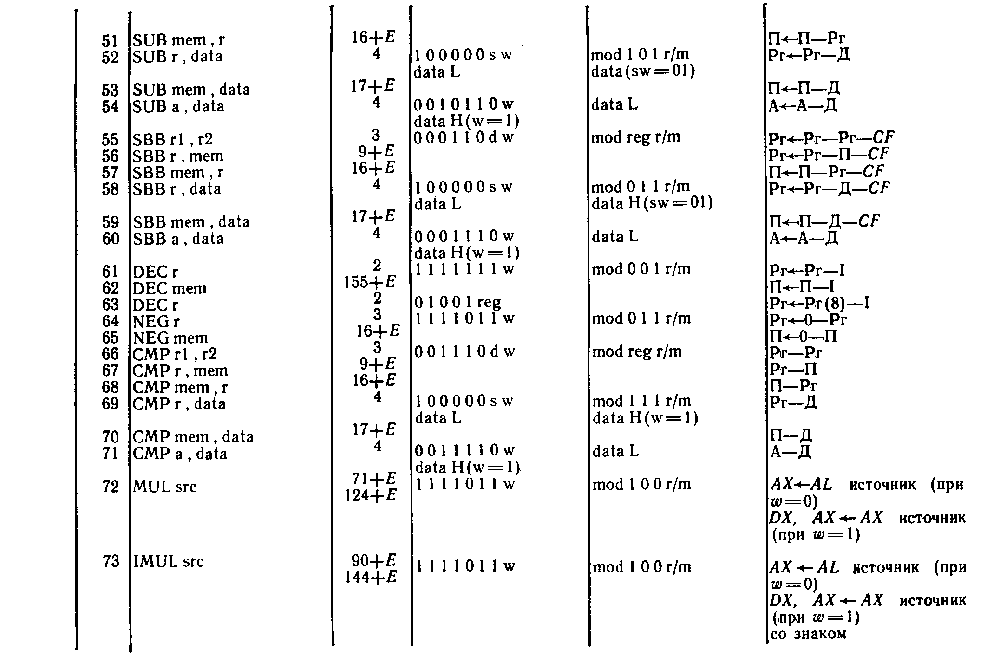
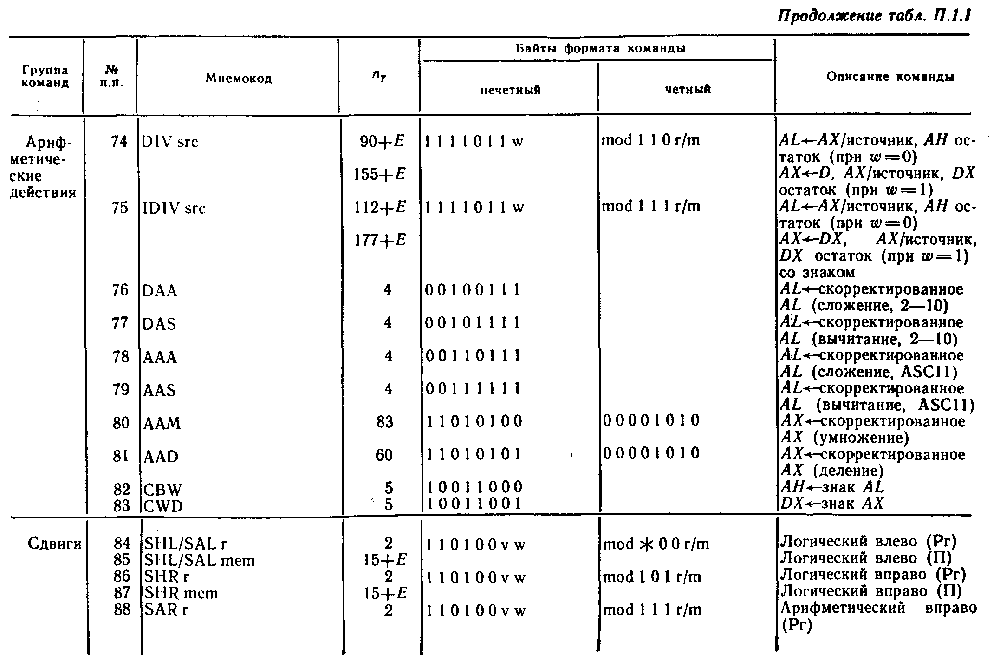
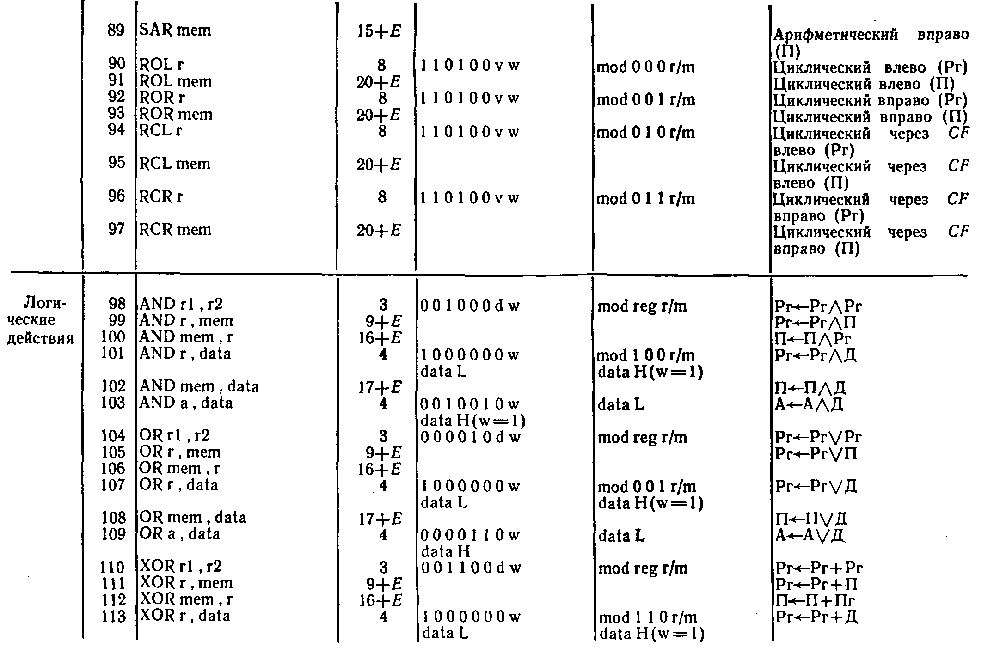
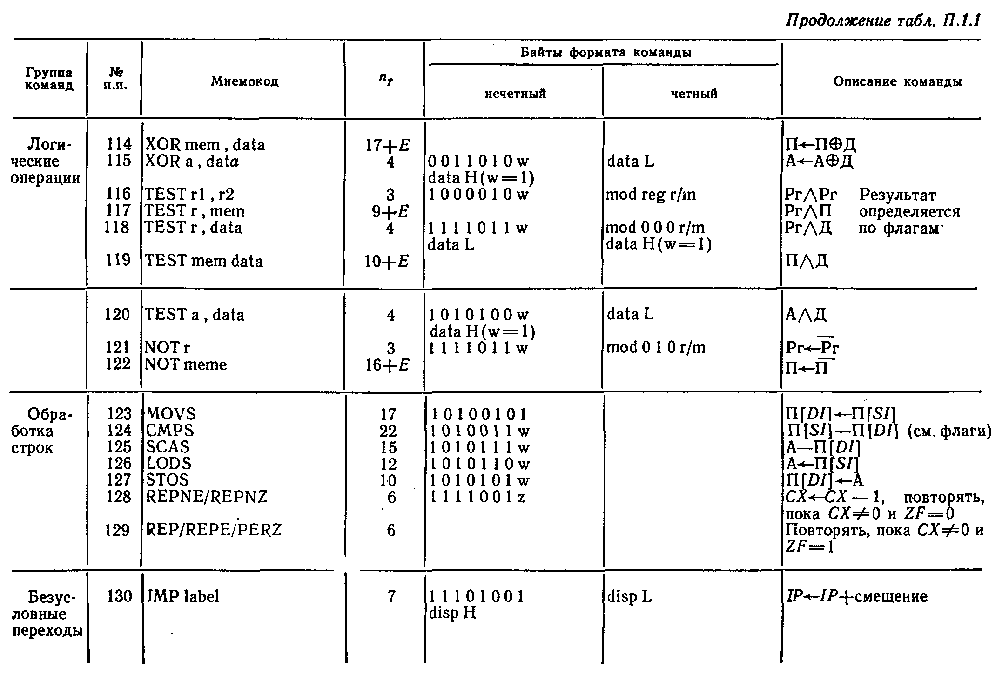
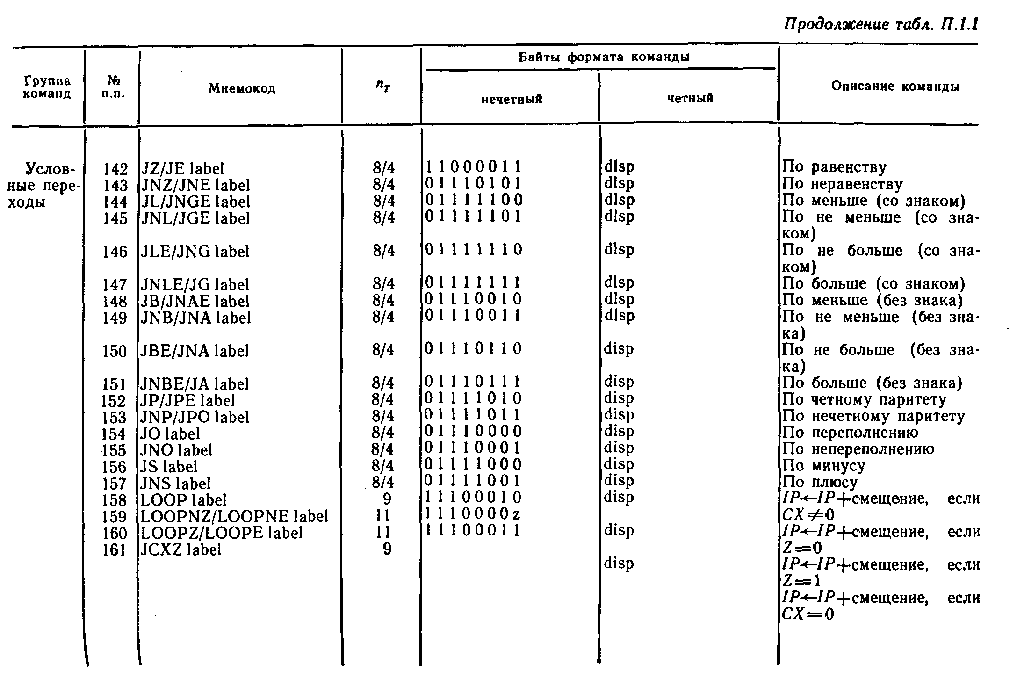
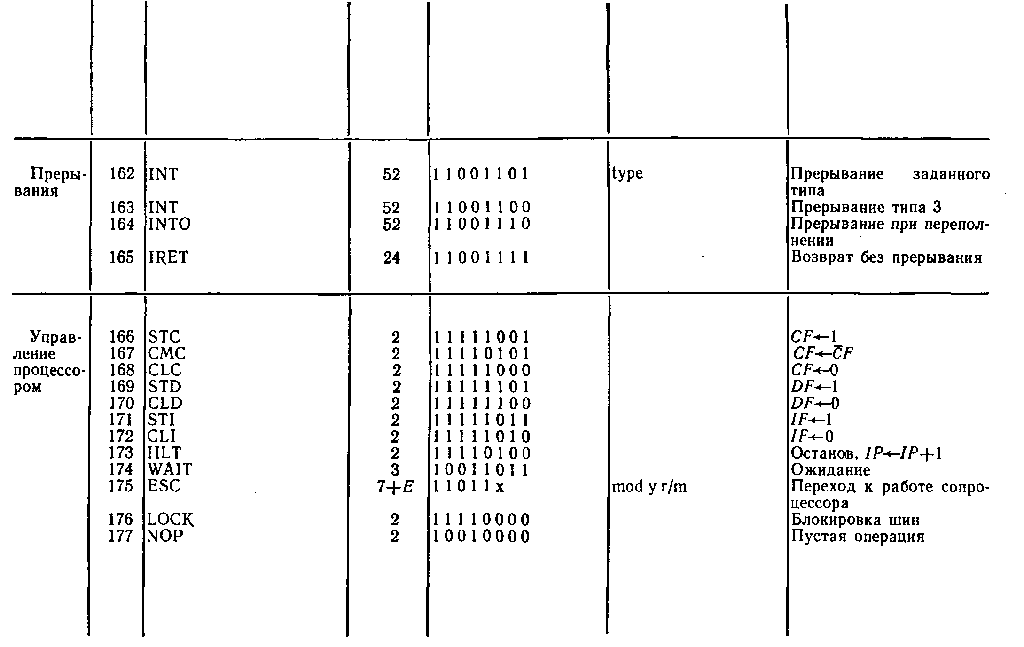
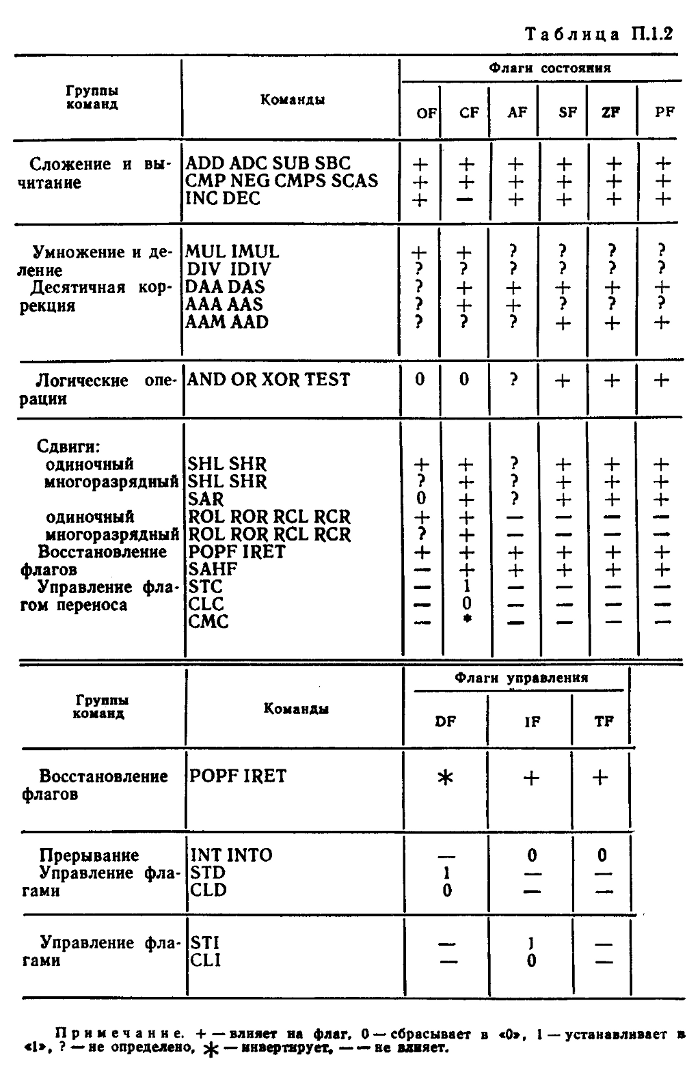
Система команд микропроцессора Intel 8086
Обозначения: пT — число тактов, требуемое для выполнения команды; Е — число тактов, затрачиваемое на вычисление исполнительного адреса ЕА операнда, находящегося в памяти; r (или rl, r2) — регистр ЦП; seg — сегментный регистр ЦП; а (или А)— аккумулятор AL или АХ; mem — ячейка памяти; data — данные, непосредственно представленные в команде (data L, data H — младший и старший байты данных); port — имя или номер порта ввода — вывода; disp — константа смещения (disp L, disp H — младший и старший байты константы смещения); label — метка (адрес метки или ее имя); name — имя подпрограммы (или ее начальный адрес); addr — адрес (addr L, addr H—младший и старший байты адреса); type — тип или уровень прерывания; mod — режим адресации; reg — код регистра; r/m—регистр/память (поле в постбайте команды); w = 0 — размерность регистра (памяти или данных) 8 разрядов, w=1—размерность регистра (памяти или данных) 16 разрядов; d=0 — пересылка из регистра, d=l — пересылка в регистр; sw = 01—16-разрядная константа, sw=ll — 8-разрядная константа; v=0 — счетчик=1, v=1 — счетчик=(СХ).