Часть первая

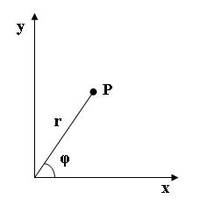
Требуется нарисовать шесть линий под углом $60^\circ$ друг с другом. Для облегчения расчетов перейдем в полярную систему координат (так как в ней естественным образом делается поворот). В полярной системе координата точки задается так же двумя числами, однако суть их несколько другая. Выбирается некоторое направление (Ox на рисунке), на нем начальная точка (начало координат в нашем случае). Координаты точки задаются парой чисел: расстоянием $\rho$ до выбранной точки и углом $\phi$ между этим отрезком $\rho$ и выбранным направлением Ох.

Между привычной декартовой и полярной системами координат можно перейти с помощью следующих формул:

$$ \begin{eqnarray} \rho & = & \sqrt{x^2+y^2} \\ \phi & = & \arccos\frac{x}{\rho} \end{eqnarray} $$ И обратно: $$ \begin{eqnarray} x & = & \rho\cos{\phi} \\ y & = & \rho\sin{\phi} \end{eqnarray} $$

С использованием полярных координат поворот линии выполняется с помощью следующего алгоритма:

1. Перевести координаты конца линии из декартовых в полярные полярные
2. Компоненте к углу $\phi$ добавить $60^\circ$.
3. Перевести координаты конца обратно из полярных в декартовые
4. Нарисовать линию на экран

users oglgraph, crt, math;
 
type point = record
  x,y,r,phi:real;
end;
 
var 
  gd, gm: smallint;
  p_nach:point; // центр снежинки, он будет неподвижен
  p_konech:point; // конец снежинки, его координата будет меняться
  x_centr, y_centr:integer; // координаты центра экрана
 
function dec2pol(p:point):point;
begin
  dec2pol.x = p.x;
  dec2pol.y = p.y;
  dec2pol.r = sqrt(sqr(p.x) + sqr(p.y));
  dec2pol.phi = arccos(p.x/dec2pol.r);
end;
 
function pol2dec(x:point):point;
begin
  //реализовать самостоятельно
end;
 
begin
  gd := Detect;
  gm := DetectMode;
  initgraph(gd, gm, '');
 
  x_centr := getmaxx div 2; // найдем центр снежинки
  y_centr := getmaxy div 2;
 
  p_nach.x := 0; // зададим координаты центра снежинки
  p_nach.y := 0;
 
  p_konech.x := 0; // и конца ее первого луча, пусть он будет вертикальный
  p_konech.y := 200;
 
  line(round(p_nach.x) + x_centr, round(p_nach.y) + y_centr, round(p_konech.x) + x_centr, round(p_konech.y) + y_centr); // нарисуем первую линию снежинки
 
  for i := 1 to 5 do
  begin
    // реализовать самостоятельно отрисовку остальных линий снежинки
  end;
  repeat until graphkeypressed;
  closegraph;
end.